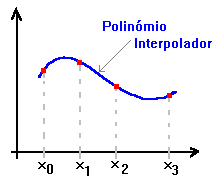
O polinómio de 3º grau interpola a função em 4 pontos
| |
Consideremos um conjunto de pontos (designados nós de interpolação) x0 , ... , xn , a que estão associados os valores de uma função: f0 , ... , fn, respectivamente. Pretendemos encontrar um polinómio p ( x ) :
| p ( xi ) = fi |

Escrevendo p( x ) = a0 + a1 x + ... + am xm, obtemos o sistema
| a0 + a1 x0 + ... + am x0m = f0 |
| ... |
| a0 + a1 xn + ... + am xnm = fn |
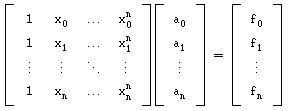
em que a matriz do sistema é conhecida como Matriz de Vandermonde.
A existência e unicidade do polinómio interpolador é equivalente a assegurar
que o sistema é possível e determinado para quaisquer
x0 , ... , xn distintos.
Teorema:
Dados n+1 nós, x0 , ... , xn
e os respectivos valores f0 , ... , fn,
existe um e um só, polinómio interpolador de grau < n,
para esses valores.
demonstração:
Agora, basta considerar a Fórmula Interpoladora de Lagrange:
Trata-se de uma fórmula alternativa para o cálculo do polinómio interpolador, baseada numa construção sucessiva a partir dos polinómios de graus inferiores.
Começamos por considerar que conhecemos a expressão do polinómio
pn-1(x) de grau < n-1 que interpola
os nós x0 , ... , xn-1.
O polinómio pn(x) de grau < n, que interpola
os nós x0 , ... , xn-1, xn,
pode-se escrever na forma:
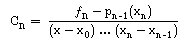
Portanto, podemos agora escrever
e podemos obter sucessivamente, a partir do polinómio interpolador de grau zero p0(x) = f0 :
| p1(x) = f0 + f [ x0 , x1 ] ( x - x0) |
| p2(x) = f0 + f [ x0 , x1 ] ( x - x0) + f [ x0 , x1, x2 ] ( x - x0) ( x - x1) |
| ... etc ... |
 |
e uma diferença dividida de ordem k, pode ser obtida a partir das anteriores :
(a regra subjacente é que no denominador vai ficar a diferença entre os nós, que não são comuns às diferenças divididas do numerador).
Observa-se que qualquer permutação da ordem dos nós não altera o resultado.
Ou seja, por exemplo,
f [ x1, x2 , x3 ] =
f [ x2, x3 , x1 ]
Nota: Podemos considerar os valores fi como diferenças divididas de ordem zero, e reparamos que isso é coerente com a definição da diferença de 1ª ordem a partir delas.
Número de operacões:
Se resolvermos o sistema linear, como vimos no Capítulo II,
é necessário efectuar um total de ~2 n3/3 operações. Usando a Fórmula de Lagrange ou
a Fórmula de Newton reduzimos para ~3 n2/2. A F. Lagrange usa mais
multiplicações+divisões que a F. Newton, que, por sua vez, usa mais somas+subtracções.
O erro de interpolação, num certo ponto x, é :
|
|
Esta fórmula é útil do ponto vista teórico, como também veremos mais tarde, no caso da integração.
Vamos, no entanto, aproveitar uma relação entre as diferenças divididas e as derivadas,
para estabelecer uma outra fórmula.
Teorema :
Consideremos n+1 nós de interpolação x0 , ... , xn
distintos entre si incluídos no intervalo [x0, xn] onde
a função f é de classe Cn.
Então
 |
Este teorema pode ser aplicado à fórmula do erro anterior, e obtemos o seguinte corolário:
Corolário :
Seja V um intervalo que contenha os nós x0 , ... , xn
e ainda o ponto x.
Se a função f fôr de classe Cn+1( V )
então temos a
seguinte fórmula para o erro de interpolação:
 |
Terminamos este parágrafo, com um exemplo de uma função em que a aproximação,
por interpolação polinomial, pode conduzir a maus resultados.
Com efeito, se considerarmos a função
f (x) = (1 + 25 x2 )-1,
e pensarmos em interpolá-la no intervalo [-1, 1], usando nós igualmente espaçados,
ao aumentarmos o número de nós, em vez de obtermos uma melhor aproximação, vamos obter uma aproximação cada vez pior, nas extremidades do intervalo!
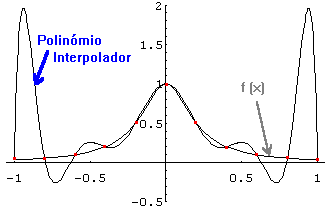
Este problema poderia ser resolvido, escolhendo nós de interpolação adequados (nós de Chebychev), mas isso sai fora do alcance deste curso.